金融工程是一門新興學(xué)科,也是一門非常熱門的專業(yè)。這一點(diǎn)相信我們今天高校里的絕大多數(shù)年輕學(xué)子都不會陌生。在許多人眼里,選讀了金融工程意味著未來的金飯碗,代表著通向輝煌與成就的大道。
金融工程的核心靈魂是什么?金融工程的核心靈魂是金融創(chuàng)新,沒有創(chuàng)新就沒有金融工程。金融工程是伴隨著金融理論和金融市場的創(chuàng)新而產(chǎn)生和發(fā)展起來的。因此金融工程是一門非常年輕的學(xué)科。在最近的二三十年的時(shí)間里迅速的發(fā)展。作為這門學(xué)科的奠基,是現(xiàn)代金融理論的發(fā)展,金融市場的完善,以及科學(xué)技術(shù)特別是信息技術(shù)的發(fā)展。
現(xiàn)代金融理論有三大支柱, 也就是資本的時(shí)間價(jià)值,資產(chǎn)定價(jià),風(fēng)險(xiǎn)管理。金融工程也有三大支柱:資產(chǎn)定價(jià),風(fēng)險(xiǎn)管理,金融工具創(chuàng)新。其中金融工具的創(chuàng)新是金融工程的核心內(nèi)容。金融工程這門學(xué)科正是伴隨著近半個(gè)世紀(jì)以來金融創(chuàng)新的步伐產(chǎn)生出來的。金融工具創(chuàng)新目前為止最為矚目的兩大成就,一個(gè)是金融衍生品,另外一個(gè)是資產(chǎn)證券化。而金融衍生產(chǎn)品相對來說出現(xiàn)更早,并且可以說是資產(chǎn)證券化的基礎(chǔ)。衍生品的發(fā)展是不僅是金融市場,也是金融工程發(fā)展的里程碑。可以說衍生品的出現(xiàn)和發(fā)展是目前金融工程最突出的成就。衍生品的妙處在于,它并沒有創(chuàng)造出一種新的基礎(chǔ)資產(chǎn),而是利用已有的基礎(chǔ)金融資產(chǎn),通過對合約的精確規(guī)定,像搭積木一樣創(chuàng)造出了源自基礎(chǔ)資產(chǎn),但是風(fēng)險(xiǎn)和回報(bào)特征都不同于基礎(chǔ)資產(chǎn)的新的金融工具。在原則上,這些衍生產(chǎn)品可以完全用基礎(chǔ)資產(chǎn)的組合進(jìn)行復(fù)制,從而使我們可以對其進(jìn)行定價(jià)。然而這些衍生品的出現(xiàn)卻為我們提供了非常有力的工具,讓市場參與者能夠更加靈活的操縱金融市場,大大擴(kuò)大了市場的參與程度,加強(qiáng)了流動性,促進(jìn)了市場更加有效和完備。
現(xiàn)代金融理論的分支大體有四個(gè)方面,即,有效巿場理論,風(fēng)險(xiǎn)和收益評估理論,資產(chǎn)定價(jià)理論,以及公司金融理論。其中資產(chǎn)定價(jià)理論是現(xiàn)代金融理論的核心,也是金融工程的重要研究對象。因此本書的前兩章作為鋪墊,詳細(xì)介紹了現(xiàn)代金融學(xué)的一些基本理論, 包括無套利均衡分析方法,MM理論,資本資產(chǎn)定價(jià)理論,以及無套利理論。其中MM理論指出在一定的條件下,包括無稅收,無發(fā)行和交易成本,無套利,有效巿場,公司的估值與公司的資本結(jié)構(gòu),也就是融資方式無關(guān)。企業(yè)的金融活動本質(zhì)上不創(chuàng)造價(jià)值。當(dāng)然,事實(shí)上這些假設(shè)在現(xiàn)實(shí)生活中并不成立。金融市場上的交易都是零凈現(xiàn)值交易。此外,公司的整體價(jià)值來源于部分的有機(jī)結(jié)合,而非簡單結(jié)合,要素的結(jié)合方式是關(guān)鍵。運(yùn)營中產(chǎn)生持續(xù)的經(jīng)營價(jià)值,停止運(yùn)營后只剩下清算價(jià)值。
資本資產(chǎn)定價(jià)理論的重要性在于它對金融風(fēng)險(xiǎn)與收益之間平衡關(guān)系的刻畫。金融決策的核心內(nèi)容是風(fēng)險(xiǎn)和收益的權(quán)衡。風(fēng)險(xiǎn)指的是預(yù)期結(jié)果的不確定性。包括系統(tǒng)風(fēng)險(xiǎn)和非系統(tǒng)風(fēng)險(xiǎn)。天底下沒有免費(fèi)的午餐,要獲得超額收益就必須承擔(dān)相應(yīng)的風(fēng)險(xiǎn),而反之并不成立。在一定的收益水平之下,存在著一個(gè)最佳也就是最低的風(fēng)險(xiǎn)水平,反之,在一定的風(fēng)險(xiǎn)水平之下,也存在這一個(gè)最佳也就是最高的收益水平,這也就是資本資產(chǎn)定價(jià)理論要告訴我們的,最佳風(fēng)險(xiǎn)與收益的關(guān)系可以用二維平面上的一條曲線也就是有效邊界來確定,而實(shí)現(xiàn)這一有效邊界,獲取最佳風(fēng)險(xiǎn)與收益組合的途徑便是通過資產(chǎn)的分散化,這也就是我們熟知的規(guī)則-雞蛋不要放在一個(gè)籃子里的理論根據(jù)。
我們要介紹的第一種衍生產(chǎn)品是遠(yuǎn)期合約。遠(yuǎn)期的基本思想和規(guī)定非常簡單-主要是在現(xiàn)金流發(fā)生的時(shí)間點(diǎn)上做文章。相對于現(xiàn)貨買賣,遠(yuǎn)期合約規(guī)定合約的買方在未來的某一特定時(shí)間以固定的價(jià)格向合約的賣方購買某種基礎(chǔ)資產(chǎn)。本質(zhì)上,遠(yuǎn)期合約是鎖定了價(jià)格和未來交易時(shí)間的基礎(chǔ)資產(chǎn)交易。那么人們?yōu)槭裁匆脒h(yuǎn)期交易呢?簡單的來說,消除未來的不確定性。由于未來的買賣和價(jià)格得到鎖定,買方不必?fù)?dān)心未來市場價(jià)格的下跌從而面臨損失或滯銷,而賣房也不必?fù)?dān)心未來價(jià)格的上漲或商品的脫銷。在農(nóng)產(chǎn)品銷售中,這種遠(yuǎn)期交易倍受青睞。農(nóng)產(chǎn)品遠(yuǎn)期交易期限往往設(shè)定在收獲季節(jié)到來之前3-6個(gè)月。在金融市場,期限的設(shè)置則往往根據(jù)標(biāo)的基礎(chǔ)資產(chǎn)或者負(fù)債的交付日期進(jìn)行設(shè)定。通過利率遠(yuǎn)期,借款人可以將未來負(fù)債的融資成本固定下來,通過匯率遠(yuǎn)期,從事外貿(mào)活動的企業(yè)可以消除由于未來匯率的不確定性而導(dǎo)致的跨國經(jīng)營活動所涉及的應(yīng)收或應(yīng)付賬款的不確定性,從而減少財(cái)務(wù)報(bào)表的波動,有助于企業(yè)的穩(wěn)定經(jīng)營。當(dāng)然,需要注意的是,由于遠(yuǎn)期合約對于買賣雙方的義務(wù)都是強(qiáng)制規(guī)定的,因此在消除了不確定性的同時(shí),也可能使得合同雙方失去獲得潛在超額收益的機(jī)會。比如在外匯市場上,由于匯率的波動也可能使得企業(yè)因?yàn)楸緡泿派祷蛸H值而使得原本超額的利潤被遠(yuǎn)期合約抵消。對于這種可能性應(yīng)當(dāng)予以正確的認(rèn)識,而不適宜以事后諸葛亮的角度來責(zé)難遠(yuǎn)期合約的有效性。

遠(yuǎn)期合約的主要缺點(diǎn)在于作為一種OTC合約,所有的條款都由交易雙方商定,缺乏標(biāo)準(zhǔn)化,因此也就缺乏流動性。如果在合約到期之前某一方由于某種原因希望取消合約則會比較困難,合約也很難轉(zhuǎn)讓給第三方。為了克服這一限制,本書討論的第二種衍生產(chǎn)品-期貨便誕生了。期貨是在交易所交易的標(biāo)準(zhǔn)化的遠(yuǎn)期合約。相對于遠(yuǎn)期合約,期貨可以在交易所交易期間任意轉(zhuǎn)讓和買賣,因此流動性大大增強(qiáng)。保證這一流動性的是三個(gè)途徑:第一是合約的標(biāo)準(zhǔn)化,包括交易的數(shù)量,交割日期,交割的實(shí)物或金融資產(chǎn)的特征等等。比如標(biāo)普500股指期貨的標(biāo)的資產(chǎn)固定為標(biāo)普500指數(shù)成分股,交割日期為3月,6月,9月和12月的第三個(gè)星期三。第二是統(tǒng)一清算,中央交易對手和會員制度。期貨的清算由交易所統(tǒng)一進(jìn)行,買賣雙方不再直接接觸,而是均通過與中央交易對手進(jìn)行。此外,只有具有會員資格的交易對手才有資格參與期貨交易。這些措施大大減少了違約風(fēng)險(xiǎn),并進(jìn)一步增強(qiáng)了期貨的流動性。第三是每日盯市和保證金制度。由于期貨價(jià)格隨著市場的變化每時(shí)每刻都在進(jìn)行波動,交易所對所有期貨合約實(shí)行盯市尺度,每天收盤時(shí)對所有期貨合約的凈值進(jìn)行計(jì)算并與前一交易日進(jìn)行比較,如果凈值超過一定闕值,則要求客戶賬戶中必須有足夠的保證金予以保證,否則將要求客戶追加保證金。如果客戶無法按照規(guī)定追加保證金則交易所對客戶的頭寸進(jìn)行強(qiáng)制平倉,從而避免風(fēng)險(xiǎn)暴露的積累。以股票為例,為什么說投資股票期貨比投資股票本身門檻要高很多呢?原因在于,期貨的高杠桿使得玩期貨比玩股票的風(fēng)險(xiǎn)高很多很多。比如,通過繳納10%的保證金,投資者可以以10倍的杠桿對股市進(jìn)行投資。花10塊錢就可以承擔(dān)價(jià)值100元股票的損益,自然具有相當(dāng)強(qiáng)的誘惑力。但是,杠桿也會帶來同樣比例的損失。并且,與股票不同的一點(diǎn)是,股票的損益只有在股票轉(zhuǎn)手時(shí)才會實(shí)現(xiàn),而在持有期內(nèi),無論股票價(jià)格如何變化,只要投資者保持淡定的心態(tài),就不必理會股價(jià)的波動。比如投資者花了100元買了一只股票計(jì)劃持有10個(gè)月,在未來的幾個(gè)月的時(shí)間里,股票價(jià)格可能會劇烈波動,比如從頭三個(gè)月從100元一路飆升到150元,然后在接下去的四個(gè)月里又暴跌到20元,最后在10個(gè)月之后又回升到120元,這中間的波動其實(shí)都與投資者關(guān)系不大,只要投資者不將股票脫手同時(shí)發(fā)行股票的企業(yè)沒有破產(chǎn)清盤,投資者最后將股票以120元的價(jià)格賣出時(shí)實(shí)現(xiàn)的收益總是20元,而不是50元或者虧損80元。從這一點(diǎn)來說,股票的投資回報(bào)可以說是與路徑無關(guān)的,也就是股票的收益僅僅與股票持有期初和期末的價(jià)格差有關(guān)。當(dāng)然我們在這里沒有考慮到股票分紅的影響。而期貨則有所不同,期貨的盯市制度使得損益會在期貨有效期內(nèi)的每個(gè)交易日實(shí)現(xiàn),并反應(yīng)到客戶的保證金賬戶。接著上面的那個(gè)例子,假如投資者通過期貨市場投資同樣股票的多頭頭寸,期貨期限為10個(gè)月,股票初始價(jià)格為100元。投資者需要付出的初始保證金為10%也就是10元,存入保證金賬戶。加入第二天股票漲到150元,投資者的保證金賬戶里就會立刻多出50元,這個(gè)時(shí)候他可以選擇平倉退出期貨合約,凈收益是50元,回報(bào)率是400%。而如果直接投資股票的收益只有50%。假如投資者選擇不平倉,第三天股票的價(jià)格突然暴跌到20元,假如維持保證金為10元,目前由于股票價(jià)格相對于初始價(jià)格下跌了80元,投資者的保證金余額虧空凈70元,為了維持頭寸,期貨交易所會要求投資者追加70元的保證金,也就是俗稱的 margin call. 前兩年的一部電影就是叫這個(gè)名字,講的是華爾街金融風(fēng)暴的故事。這筆多追加的保證金是投資者最初投資額的7倍。如果投資者無法追加這筆額外的保證金,期貨交易者就會強(qiáng)制平倉。投資者構(gòu)成了事實(shí)上的違約。即使到期貨合約到期之后股票的價(jià)格高于最初的價(jià)格,比如120元,投資者如果能夠堅(jiān)持到最后依然可以實(shí)現(xiàn)凈獲利20元或者200%的凈回報(bào)率,但投資者可能根本撐不到那個(gè)時(shí)候就已經(jīng)被 margin call擊殺在半路上了,依然無法能夠笑到最后。事實(shí)上,這種情況在期貨市場上每天都在上演,無論是機(jī)構(gòu)還是個(gè)人,都有可能在瞬間暴富,或者在瞬間血本無歸。有的人甚至由于盲目的入市期貨市場而買房買車,搞得債臺高筑,眾叛親離。造成這些悲劇的主要根源,其實(shí)是缺乏對流動性風(fēng)險(xiǎn)的有效管理。事實(shí)上,許多企業(yè)破產(chǎn)并不是因?yàn)橘~面上資不抵債,相反,企業(yè)的權(quán)益資本可能相當(dāng)?shù)某渥悖Y產(chǎn)質(zhì)量也并沒有出現(xiàn)根本的惡化,但往往是由于缺乏現(xiàn)金流來償還立即到期的債務(wù),而且又無法通過將資產(chǎn)迅速變現(xiàn)來籌集資金,因而導(dǎo)致破產(chǎn)清算。當(dāng)然,解決這一問題有一些方法,比如通過資產(chǎn)證券化,這牽涉到金融工程領(lǐng)域里又一個(gè)非常有意思的話題,由于本書沒有涉及我們在這里也就不展開了。
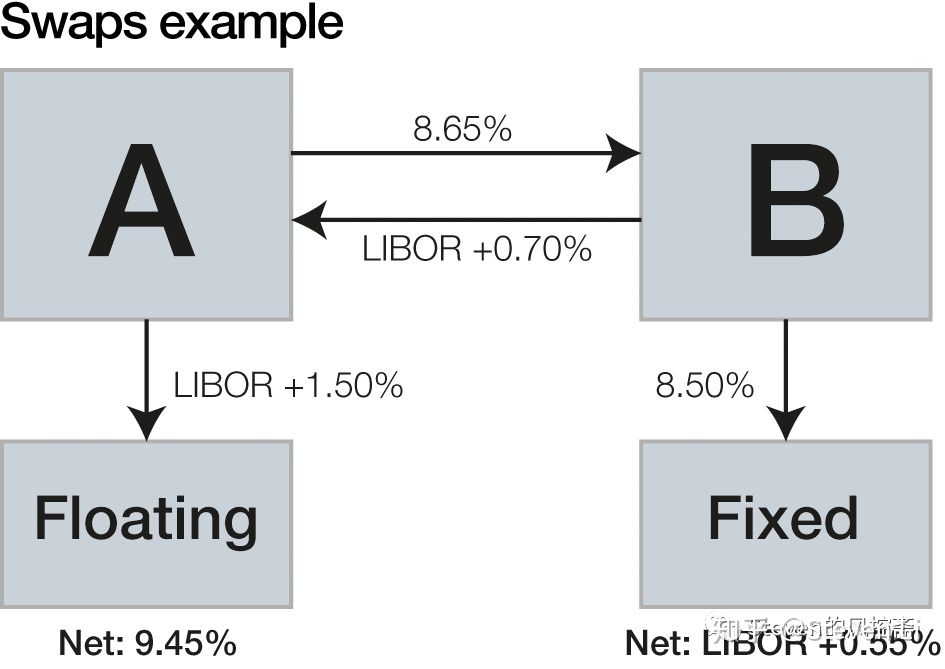
我們介紹的下一種衍生品是掉期,掉期又稱為互換。本質(zhì)上,掉期是一系列遠(yuǎn)期交易的加和,在實(shí)際應(yīng)用中,掉期往往比遠(yuǎn)期更加普遍。這并不難理解。金融資產(chǎn),特別是固定收益類產(chǎn)品,其支付往往都會涉及跨越某個(gè)期限的一系列,而不是單個(gè)現(xiàn)金流。掉期合約可以將這一系列現(xiàn)金流在不同的貨幣種類之間互換,也可以在固定與浮動利率之間互換,甚至可以在不同的浮動利率之間互換。從資產(chǎn)和負(fù)債的角度,相當(dāng)于把一種資產(chǎn),比如固定利率債券,交換為另一種資產(chǎn),比如浮動利率債券,或是以美元為支付貨幣的債券交換為歐元為支付貨幣的債券。這樣的好處是什么呢? 其中一種是利用比較優(yōu)勢降低掉期合約雙方的融資成本一個(gè)例子來說明,A企業(yè)的評級是AAA, 它可以以LIBOR+50bp的浮動利率或3%的固定利率融資。B企業(yè)的評級是BBB, 它可以以LIBOR+200bp的浮動利率或5%的固定利率融資。注意這里A企業(yè)由于具有較高的信用評級,不管以固定還是浮動利率融資都具有絕對的優(yōu)勢,也就是較低的融資成本。但是這種優(yōu)勢對于浮動利率是150個(gè)基點(diǎn)的利差,而對于固定利率利差則高達(dá)200個(gè)基點(diǎn)。也就是說,A企業(yè)相對于B企業(yè),具有固定利率融資的比較優(yōu)勢,而B企業(yè)相對于A企業(yè)則具有浮動利率的比較優(yōu)勢。現(xiàn)在假如A企業(yè)希望以浮動利率融資1000萬,B企業(yè)希望以固定利率融資1000萬。假如他們以各自的融資成本直接進(jìn)行借貸,總共要付出的利息是LIBOR +550基點(diǎn)。反之,假如A和 B 分別以固定和浮動利率進(jìn)行融資,再進(jìn)行一個(gè)掉期互換協(xié)議,A以3%融資,同時(shí)根據(jù)掉期協(xié)議支付給B LIBOR, B以LIBOR+200bp融資,同時(shí)根據(jù)掉期協(xié)議支付給A 280bp, 這樣A 的凈融資成本是LIBOR+20bp, B的凈融資成本是4.8%, 與直接融資相比,A與B分別節(jié)約30bp和20bp的成本,總共節(jié)約50bp, 根據(jù)2000萬的總?cè)谫Y額就是10萬元。所以,通過掉期協(xié)議,可以使得協(xié)議雙方各取所需,互利互惠。
當(dāng)代金融工程最重要,最復(fù)雜的衍生品是期權(quán)。期權(quán)是當(dāng)代金融工程的核心。幾乎任何復(fù)雜一些的金融產(chǎn)品都會直接或間接的包含期權(quán)的性質(zhì)和特征。期權(quán)的定價(jià)和對沖理論,是所有金融工程和金融數(shù)學(xué)專業(yè)的核心課程,期權(quán)業(yè)務(wù)也是許多大型金融機(jī)構(gòu),無論是買方還是賣方的核心業(yè)務(wù)之一。
期權(quán)(option)有兩種基本形式,也就是看漲(call)和看跌(put)期權(quán)。看漲期權(quán)允許期權(quán)的買方在期權(quán)期限末以事先敲定的價(jià)格從期權(quán)的賣方那里購買一定數(shù)量的標(biāo)的資產(chǎn),比如股票。與此對應(yīng),看跌期權(quán)則允許期權(quán)的買方在期權(quán)期限末以事先敲定的價(jià)格向期權(quán)的賣方那里出售一定數(shù)量的標(biāo)的資產(chǎn)。顯然,看漲期權(quán)在標(biāo)的資產(chǎn)價(jià)格上漲的時(shí)候會盈利,而看跌期權(quán)的盈利時(shí)機(jī)則是在標(biāo)的資產(chǎn)下跌之時(shí)。有趣的是,如果將兩者結(jié)合,也就是一個(gè)看漲期權(quán)的多頭與一個(gè)看跌期權(quán)的空頭結(jié)合起來,總的頭寸的盈虧狀況與同樣標(biāo)的資產(chǎn)的一個(gè)遠(yuǎn)期合約的買權(quán)相同。這一關(guān)系,也就是著名的 put-call parity , 是期權(quán)的一個(gè)基本定律,它是一個(gè)適用范圍很廣的關(guān)系,并且與具體的模型無關(guān)。

通過這一關(guān)系,如果我們能夠通過某種方法,比如后面講到的二叉樹方法或者 Black-Scholes 模型得到看漲和看跌期權(quán)其中之一的價(jià)格,那么根據(jù)二者的這一關(guān)系,我們可以立刻得到另外一種期權(quán)的價(jià)格。因此,只要知道如何對看漲期權(quán)定價(jià),我們也就可以得到看跌期權(quán)的價(jià)格,反之亦然。
投資看漲或看跌期權(quán),投資者可以比直接投資于標(biāo)的資產(chǎn)獲取更高的杠桿率,也就是成比例的放大損益。這使得期權(quán)的投資具有很高的風(fēng)險(xiǎn)性。同時(shí),與我們上文中提到過的其他幾種衍生品,如期貨和遠(yuǎn)期不同,期權(quán)的權(quán)利義務(wù)關(guān)系是單向的。對于買方而言,期權(quán)是一種權(quán)利而非義務(wù)。它允許持有者在對自己有利的情況下行權(quán),從而規(guī)避風(fēng)險(xiǎn)或獲得收益,同時(shí)可以在對自己不利的情況下選擇不行權(quán)從而避免損失。反之,對于買方而言,期權(quán)是一種單純的義務(wù)。如果對方選擇行權(quán),己方就一定要履行義務(wù)。這種情況下的潛在風(fēng)險(xiǎn)可能很大,比如看漲期權(quán),由于股票的價(jià)格可以無限飆升,賣方的損失實(shí)際上是無上限的。因此,作為回報(bào),期權(quán)的買方必須支付給買方一筆期權(quán)金。如何確定這筆期權(quán)金的數(shù)額,也就是給期權(quán)定價(jià),是期權(quán)研究的核心問題。
關(guān)于各種基于期權(quán)組合的各種交易策略,要點(diǎn)在于各種期權(quán)到期的損益隨著股票價(jià)格的不同的變化。而這些歸根到底無非是掌握四種基本期權(quán)頭寸的支付函數(shù),也就是期權(quán)到期的損益與到期股票價(jià)格的變化。這四種基本期權(quán)頭寸包括看漲期權(quán)的多頭和空頭,以及看跌期權(quán)的多頭和空頭。通過這些期權(quán)頭寸的組合,我們可以使得總的組合頭寸的盈利場景集中在到期股票價(jià)格的某一個(gè)區(qū)間,或是使得其盈利場景分散在股票價(jià)格分布的兩端。這兩種情況本質(zhì)上是基于對股票價(jià)格變動幅度,也就是波動性的交易策略,前者只有在到期股票價(jià)格不發(fā)生變化或者變化幅度極小的情況下盈利,而后者正好相反,只有在到期股票價(jià)格發(fā)生較大變化的時(shí)候才會盈利,并且盈利的幅度隨著股票價(jià)格變化幅度遞增。在上述的兩種情況下,股票價(jià)格變動的幅度而非變動的方向是決定盈虧的主要因素。股票價(jià)格具體是大幅上漲和大幅下跌,對于組合盈虧的影響是類似的。因此,這種組合在本質(zhì)上是對于股票價(jià)格波動率的看空或者看跌,而非對于標(biāo)的資產(chǎn)的股票價(jià)格本身的看空或者看跌。

期權(quán)的定價(jià)是討論各種與期權(quán)相關(guān)的問題的核心。幾乎任何一本金融工程的書籍都繞不開對于期權(quán)定價(jià)問題的討論。而期權(quán)定價(jià)問題的核心是無套利原理。通過合適的策略,總是可以將期權(quán)的損益用合適數(shù)量的標(biāo)的資產(chǎn)以及無風(fēng)險(xiǎn)債券來復(fù)制,這種復(fù)制策略不僅是期權(quán)可以被精確定價(jià)的基礎(chǔ),也是期權(quán)風(fēng)險(xiǎn)可以被完美對沖的依據(jù)。教科書上經(jīng)常提到的兩種期權(quán)定價(jià)方法,二叉樹和Black-Scholes模型,都是基于無套利和完美復(fù)制的原理進(jìn)行定價(jià)的。具體來講,要完美復(fù)制期權(quán)的損益,就必須選擇合適的標(biāo)的資產(chǎn)數(shù)量,使得這一定標(biāo)的資產(chǎn)數(shù)量在總價(jià)格上的變化正好可以抵消被復(fù)制期權(quán)在價(jià)格上的變化。由于期權(quán)的杠桿性質(zhì),這一復(fù)制期權(quán)損益所需的標(biāo)的資產(chǎn)數(shù)量一般來說是一個(gè)小于1的正數(shù),稱為delta, 描述的是期權(quán)價(jià)格對于標(biāo)的資產(chǎn)價(jià)格的敏感性。而基于這一方法的對沖策略習(xí)慣上稱為delta- 對沖。需要說明的是,二叉樹作為一種將股票未來價(jià)格變化離散化的方法,是一種近似直觀的定價(jià)方法。它的優(yōu)點(diǎn)是直觀,便于理解和實(shí)現(xiàn),并且可以用來同時(shí)對歐式和美式期權(quán)進(jìn)行定價(jià)。我們知道,美式期權(quán)與歐式期權(quán)的不同點(diǎn)在于其行權(quán)時(shí)間可以是從期權(quán)交割日開始到期權(quán)到期日為止的任一交易日都可以實(shí)施行權(quán),而歐式期權(quán)只有在期權(quán)到期日當(dāng)天才可以行權(quán)。因此,美式期權(quán)賦予了投資者更大的靈活性,因此其價(jià)格一般也要高于同樣條件下的歐式期權(quán)。二叉樹方法可以在每個(gè)樹叉節(jié)點(diǎn),也就是代表著未來某個(gè)時(shí)間點(diǎn)和某一股票價(jià)格的狀態(tài)上,對未來繼續(xù)持有和當(dāng)期行權(quán)的現(xiàn)金流進(jìn)行比較,從而進(jìn)行決策。

我們可以舉一個(gè)簡單的例子來直觀的了解二叉樹進(jìn)行期權(quán)定價(jià)的原理。假如你作為某個(gè)賭場的莊家,為你的賭客們提供如下的兩種擲骰子的游戲。第一種:投擲兩次骰子,第二次投擲結(jié)束以后,你的收益是第二次擲到的骰子的點(diǎn)數(shù)與4的差,如果這個(gè)差為正數(shù),否則為0. 第二種:第一次擲完骰子以后,你可以選擇結(jié)束游戲,也可以選擇繼續(xù)第二次骰子,無論怎樣,當(dāng)游戲結(jié)束的時(shí)候收益規(guī)則與第一種游戲相同。問題是:莊家應(yīng)該向賭客收取多少費(fèi)用來玩這兩種游戲。第一種游戲顯然是一個(gè)歐式期權(quán)的定價(jià)問題。第一次投擲骰子沒有任何意義,在第二次投擲之后骰子可能是1-6點(diǎn)的任何一種情況,每種情況的概率是1/6. 其中只有在骰子擲到5點(diǎn)或6點(diǎn)時(shí)才會有正的收益。因此最后游戲的平均收益為0.5元。在風(fēng)險(xiǎn)中性,也就是投資者沒有任何風(fēng)險(xiǎn)偏好的假設(shè)下,這也就是該游戲的公允價(jià)格。第二個(gè)游戲則要復(fù)雜一些,因?yàn)樗诒举|(zhì)上是一個(gè)美式期權(quán)的定價(jià)問題。我們可以做如下的分析。我們已經(jīng)知道擲第二次骰子的期望收益是0.5元。因此只有在擲第一次骰子的收益高于0.5元的時(shí)候才應(yīng)該終止游戲,否則就應(yīng)該繼續(xù)擲第二次骰子。擲一次骰子收益高于0.5元的情況有兩種,即5和6,收益分別為1和2, 期望收益,也就是二者的平均值為1.5. 如果骰子為1,2,3,4點(diǎn)時(shí)則應(yīng)該繼續(xù)游戲,期望收益為0.5 。因此,我們以2/3的概率得到期望收益0.5, 1/3的概率得到期望收益1.5,總的期望收益為2/3*0 .5 + 1/3*1.5=5/6, 約為0.83. 與第一種游戲相比,第二種游戲的期望收益更高,因此莊家的價(jià)格為0.83 。兩者的差值為0.33, 或者是67%。這個(gè)差值就是提前行權(quán)的價(jià)值。當(dāng)然,實(shí)際的二叉樹模型更加復(fù)雜。分差的步數(shù),也就是樹的深度,往往超過2步。但是基本的思想與上面講到的擲骰子游戲是類似的。

相對于二叉樹模型,Black-Scholes 模型建立在更加嚴(yán)格的數(shù)學(xué)基礎(chǔ)上,具體的來說,Black-Scholes 模型是期權(quán)價(jià)格所滿足的一個(gè)二階倒向偏微分方程的解。這一方程的建立,來源與上面講到的二叉樹模型類似,都是基于無套利和動態(tài)復(fù)制原理。談到Black-Scholes 模型,其實(shí)是由 Black, Scholes以及Merton 三位經(jīng)濟(jì)學(xué)大師共同提出并建立的。因此在有些文獻(xiàn)和書籍中也會把這個(gè)模型稱為Black-Scholes-Merton模型,或者簡稱BSM模型。BSM模型不僅是期權(quán)定價(jià),也是金融工程,乃至整個(gè)金融學(xué)發(fā)展史上里程碑式的事件。在金融和經(jīng)濟(jì)學(xué)領(lǐng)域中,這也是少數(shù)幾個(gè)理論研究領(lǐng)先于市場實(shí)踐的例子之一。這一公式揭示了無套利分析原理與隨機(jī)微積分方法在金融領(lǐng)域中的強(qiáng)大應(yīng)用。該模型于1973年問世后不久,便被編制成計(jì)算機(jī)程序運(yùn)行在新成立不久的芝加哥期貨交易所的交易中心用于場內(nèi)期權(quán)的報(bào)價(jià)。在該模型誕生不久,便誕生了各種延伸的版本,比如Merton在1975年對該模型進(jìn)行修正將其應(yīng)用于信用違約風(fēng)險(xiǎn)分析中, Hagen等人則將其推廣應(yīng)用到外匯期權(quán)的定價(jià)。由于該模型在金融中扮演的重要角色,模型的兩位創(chuàng)建者,Scholes和 Merton被授予1995年的諾貝爾經(jīng)濟(jì)學(xué)獎(jiǎng)。不幸的是,另外的一位先驅(qū)者 Black由于在頒獎(jiǎng)時(shí)已經(jīng)仙逝,沒有能夠享受到此殊榮。不能不說是一種遺憾。說起Fisher Black這個(gè)人,不愧是一位多產(chǎn)的金融學(xué)術(shù)大腕。他曾經(jīng)供職于著名的頂級投行高盛,他的另一項(xiàng)以他命名的工作是一種基于短期利率隨機(jī)過程的稱為BDT(Black-Dermen-Toy)利率模型。

期權(quán)中最重要的一個(gè)參數(shù)是波動率。它的深刻內(nèi)涵遠(yuǎn)遠(yuǎn)超過某一種具體的標(biāo)的資產(chǎn),比如股票或利率。一個(gè)有趣的現(xiàn)實(shí)是,期權(quán)的價(jià)格總是隨著波動率的增加而增加,無論是對于看漲還是看跌期權(quán)均是如此。這一點(diǎn)與Black-Scholes模型公式中出現(xiàn)的其他變量是完全不同的。這一結(jié)論無論在理論還是實(shí)踐中都非常重要的。原因在于,期權(quán)與波動率的這一單調(diào)關(guān)系決定了在其他變量,如標(biāo)的資產(chǎn)價(jià)格,敲定價(jià)格,期權(quán)期限,無風(fēng)險(xiǎn)利率等都固定的前提下,期權(quán)的價(jià)格與波動率是一一對應(yīng)的,給定了一個(gè)波動率,根據(jù)Black-Scholes模型,對應(yīng)著一個(gè)唯一的期權(quán)價(jià)格,反之亦然。也就是說,波動率與期權(quán)價(jià)格在某種意義上是等價(jià)的。因此,在市場上交易員報(bào)價(jià)時(shí)往往使用波動率而非期權(quán)價(jià)格進(jìn)行報(bào)價(jià)。這一波動率被稱為隱含波動率。

需要指出的是,即使實(shí)際期權(quán)的價(jià)格并不符合 Black-Scholes 模型,仍然不影響隱含波動率作為一種強(qiáng)大的工具在市場中的應(yīng)用。那么問題在于,真實(shí)的歐式期權(quán)是否符合Black-Scholes模型呢?這個(gè)問題很有意思。其實(shí)這一問題的等價(jià)形式可以表述如下:不同敲定價(jià)格對應(yīng)的隱含波動率是否相同為一個(gè)常數(shù)。如果我們把不同敲定價(jià)格對應(yīng)的隱含波動率在二維直角坐標(biāo)系繪制成一條曲線,便得到了通常所稱的波動率微笑(volatility smile)。在1987年之前的股票期權(quán)市場,波動率微笑對應(yīng)的是一條近似水平直線的曲線,也就是說隱含波動率在不同敲定價(jià)格下對應(yīng)的是一個(gè)常數(shù),在這種情況下,可以認(rèn)為期權(quán)價(jià)格基本服從Black-Scholes 模型。1987年10月美國股市發(fā)生了著名的黑色星期五崩盤事件,道瓊斯指數(shù)在1天內(nèi)狂瀉23%。從此之后,市場上觀測到波動率微笑曲線開始顯著偏離水平直線,開始呈現(xiàn)向右下方傾斜的趨勢,也就是隱含波動率隨著敲定價(jià)格的增加而遞減。這種趨勢被稱為波動率傾斜(volatility skew). 這意味著,敲定價(jià)格低于股票現(xiàn)價(jià)的看跌期權(quán)的價(jià)格要高于根據(jù)Black-Scholes模型計(jì)算出來的理論價(jià)格。造成這種波動率傾斜的原因在于市場在經(jīng)歷了1987年10月的黑色星期五之后,對于股市的閃崩有一種擔(dān)憂的情緒。這種情緒導(dǎo)致了市場參與者對于可以為他們的多頭股票倉位提供保護(hù)的看跌期權(quán),尤其是敲定價(jià)格遠(yuǎn)低于股票現(xiàn)價(jià)的看跌期權(quán)產(chǎn)生了強(qiáng)烈的需求。這種需求導(dǎo)致了這些看跌期權(quán)的價(jià)格,也就是隱含波動率被抬高,從而產(chǎn)生了波動率傾斜。近20年來,如何定量描述隱含波動率的規(guī)律,特別是波動率傾斜和波動率微笑,已經(jīng)成為量化金融研究前沿的一個(gè)熱點(diǎn)問題,每年都有大量的專著和文獻(xiàn)予以論述。大家如果有興趣,可以自行搜索網(wǎng)上的文獻(xiàn)。這里不再進(jìn)一步贅述。其實(shí),類似的這種市場價(jià)格中蘊(yùn)藏的“隱含量”并非僅此一例。金融危機(jī)之前一度火爆的CDO,其定價(jià)往往與標(biāo)的資產(chǎn)之間的違約相關(guān)性有一一對應(yīng)的關(guān)系,因此由此產(chǎn)生了基于"隱含相關(guān)系數(shù)" (確切來說是Base Correlation)的Bespoke CDO定價(jià)框架。這里的Bespoke CDO類似于奇異期權(quán),而標(biāo)準(zhǔn)的CDO類似于普通歐式期權(quán)。
最后要指出的是,期權(quán)的存在形式并不局限于一種,它可以以獨(dú)立形式的合約存在,也可以嵌套在其他的基礎(chǔ)資產(chǎn)當(dāng)中。比如近幾年 經(jīng)常在財(cái)經(jīng)媒體上出現(xiàn)的可轉(zhuǎn)債,它的本質(zhì)就是在基礎(chǔ)債券中加入一個(gè)可轉(zhuǎn)換為股票的期權(quán),因此這種債券的收益率往往比普通債券要低一些,原因在于投資者在其中支付了隱含期權(quán)的費(fèi)用。另外,在房貸資產(chǎn)證券化中經(jīng)常提到的提前支付風(fēng)險(xiǎn),來源于房屋按揭貸款的借貸者選擇提前還款從而避免支付利息,而這種選擇權(quán)等于賦予了借貸者了一種隱含的利率期權(quán)(prepayment option),在市場利率低于房屋固定利率時(shí)選擇行權(quán),提前還款并轉(zhuǎn)而重新借貸一筆利率更低的貸款。這對于按揭貸款支持證券(MBS)的投資者來說是一種風(fēng)險(xiǎn)。如何量化并管理這一風(fēng)險(xiǎn)依然需要借用期權(quán)定價(jià)的分析方法。






