絮叨
學校短學期剛結束了,離學校開學還有很多天,一直呆在寢室玩游戲豈不是浪費了大好時光,于是心血來潮想看看HashMap的源碼。雖然我沒有經歷過面試,但是JAVA程序員都知道,HashMap是面試官必問的知識點,而我現在只停留在對HashMap的基本使用層面,因此我覺得有必要深入了解一下HashMap的底層原理。在HashMap中,我覺得最難的應該是紅黑樹了吧,我結合代碼和畫圖軟件研究了兩天,終于總結出規律,現在分享給大家
一、紅黑樹的特點
下面是紅黑樹的5條性質,現在大家要對這些性質有印象,后面我會結合圖解的形式,多次提到這些性質來幫助大家記憶
- 每個節點要么是紅的,要么是黑色的
- 跟節點一定是黑色的
- 葉子節點一定是黑色的(葉節點一般不畫,在末尾節點上,沒有內容)
- 紅節點下的兩個子節點一定是黑色的
- 任意一條從根節點到葉子節點的路徑中黑色節點的個數相等
紅黑樹插入節點后,若導致紅黑樹不平衡(整棵樹不滿足上面5條性質中的任意一條),就會進行變色、旋轉操作,直到紅黑樹平衡,而學習紅黑樹的難點正是這些變色、旋轉的規則
二、紅黑樹的優點
談到紅黑樹的優點,就不得不拿出AVL樹來進行比較。
AVL樹是完全平衡的樹,根的最大深度和最小深度相差不大于1,查找效率比較高,而紅黑樹不是完全平衡樹,查找效率略低于AVL樹
紅黑樹的插入和刪除操作比AVL樹快很多,因為紅黑樹保證插入刪除時最多需要旋轉三次就可以達到平衡,而AVL樹每次插入刪除會進行大量的平衡度計算,開銷很大
因此,紅黑樹犧牲了一點點查找效率,使它有更快的插入刪除操作,綜合來說,紅黑樹性能高于AVL樹
三、紅黑樹插入如何平衡
3.1 紅黑樹插入基本規則
- 新插入的節點是紅的
- 父節點是黑的,或者父節點是根節點,直接插入
- 父節點是紅的,需要變色、旋轉(也就是出現兩個連在一起的紅節點失去平衡)
- 如果一次平衡后出現祖父節點和祖父節點的父親是紅的,那么把祖父節點當做新節點,繼續變色翻轉,知道整體平衡(遞歸思想)
3.2 紅黑樹變色規則
在基本規則中提到,出現兩個連續的紅節點需要變色,旋轉,所以我們暫且先不管要不要旋轉,先來看看紅黑樹的變色規則是怎么樣的吧
3.2.1 新節點沒有叔叔節點,或者叔叔節點是黑的
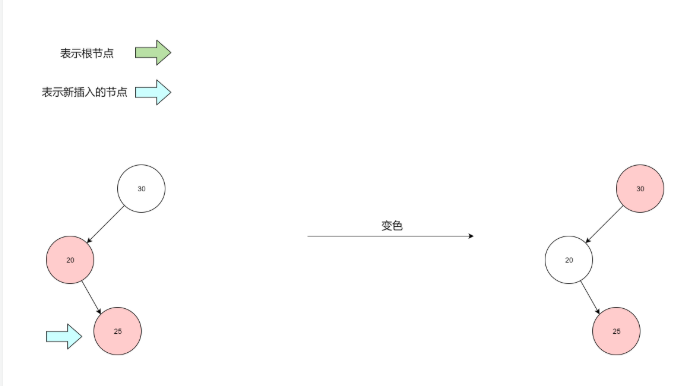
這種情況只要把父節點變黑,祖父節點變紅就ok了

這種情況不但要把父節點變黑,祖父節點變紅,還要考慮祖父節點是否是根節點,在紅黑樹插入基本規則第二條中寫到,根節點一定是黑的,所以如果祖父節點是根節點,需要再次變色把根節點顏色變黑
3.2.2 新節點的叔叔節點是紅的
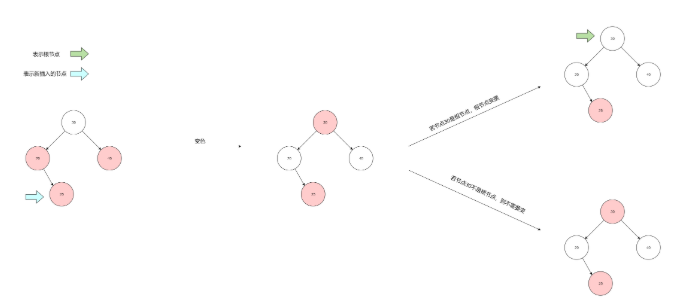
這種情況把叔叔節點和父節點顏色變黑,祖父節點變紅,變完之后還要考慮祖父節點是否是根節點,根據情況再次變色
3.2.3 小結
- 因為新節點是紅色的,所以當父節點是紅色時,出現了連續的紅節點,導致不平衡,要進行變色
- 要變色的情況下,叔叔節點和父節點一定要變黑,叔叔節點沒有就不考慮它,祖父節點要變紅
- 祖父節點變紅以后,需要考慮它是否是根節點,如果是根節點,根節點要變黑
3.3 紅黑樹旋轉規則
在上一節我們搞明白了紅黑樹是如何變色的,現在來看看紅黑樹的旋轉規則,在這一環節,變色的過程就不再具體描述了,我只描述紅黑樹如何旋轉
紅黑樹旋轉有四種情況:
- 左旋
- 右旋
- 先左旋,再右旋
- 先右旋,再左旋
左旋和右旋其實是差不多的,只是方向換了,如果看完左旋你能想到右旋是如何進行的,那么說明我寫的還是很通俗易懂的
3.3.1 左旋
首先有兩種情況下會進行左旋操作
- 新節點、父節點都在右
- 父節點在左,新節點在右
第二種情況比較復雜,等我寫完左旋和右旋操作后,再來考慮這種情況,因為他要涉及到左旋和右旋兩步操作
這里先來看一下新節點、父節點都在右的情況下是如何左旋的
圖解1
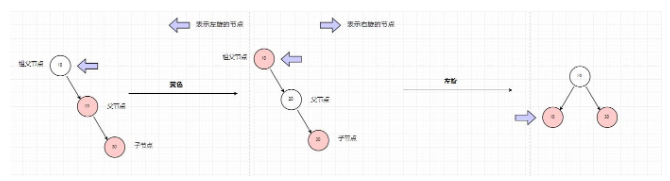
這種情況下左旋的節點都是祖父節點,祖父節往左轉成為了父節點左孩子(因為在左邊自然而然成為左孩子啦)
圖解2

這種情況稍微有點復雜,也是祖父節點往左旋轉,成為父節點的左孩子
可是原來父節點是有左孩子的(也就是兄弟節點),那么這個兄弟節點就成了祖父節點的右孩子(可以這么想,祖父節點左旋轉后,兄弟節點在右邊,因此成了他的右孩子)。
還有一點是原來祖父節點是有父親的(這里我們叫做祖先節點),如果祖先節點的左孩子是祖父節點,那么旋轉后祖先節點的左孩子變成了父節點;如果祖先節點的右孩子是祖父節點,那么旋轉后祖先節點的右孩子變成了父節點(可以這么想,父節點移到了祖父節點的位置)
3.3.2 右旋
這里也有兩種情況下會進行右旋操作
- 新節點、父節點都在左
- 父節點在右,新節點在左
右旋的操作根左旋很相似,只是方向換了一下,我這里就不再詳細的解釋了,大家看圖自己領悟,最好是把左旋看明白,在自己想想對應的情況下右旋應該怎么操作,想到了再和我下面的圖對照一下看是否正確
圖解1
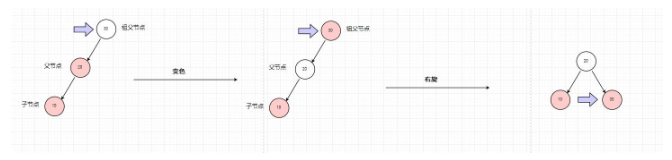
圖解2

3.3.3 先左旋,再右旋
這種情況比較復雜,不多逼逼,直接上圖
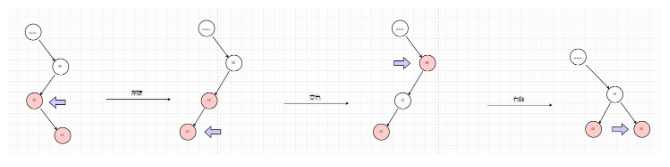
如何理解?
可以看到,新節點、父節點、祖父節點不在同一條直線上,從圖中可以看出這種情況的操作思想是先把這三個節點旋轉到一條直線上,再應用我們上面所講的左旋和右旋,來達到平衡,所以就有兩步旋轉操作了
第一步旋轉
第一步旋轉的旋轉節點和上面小節的節點不一樣,上面小節里旋轉的是祖父節點,而這里旋轉的是父節點(父節點左旋下來,子節點左旋上去)
第二步旋轉
第二步旋轉就是上面講到的右旋,自己慢慢體會
如何記憶?
這里我們怎么看的圖就想到先左旋還是先右旋呢,教你一個方法,看父節點在哪邊,父節點在左邊,左旋,父節點在右邊,右旋,這樣是不是就很簡單了呢
變色過程
之前變色過程都是在第一步做的,但這種情況是在第二步做的,所以我們看到這種圖時就要這樣想,左旋+變色+右旋,這樣就很容易記住了
3.3.4 先右旋,再左旋
這種情況也是和先左旋再右旋差不多的,只是方向變了一下,這里不過多贅述,大家看圖慢慢體會
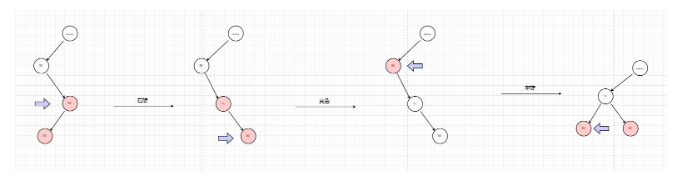
3.3.5 小節
- 當祖父節點、父節點、新節點在一條直線上,發生左旋和右旋,父節點和子節點在左,右旋;父節點和子節點在右,左旋
- 當祖父節點、父節點、新節點不在一條直線上,先旋轉父節點,使它與子節點都在左或都在右,再變色,再旋轉。父在左,左旋+變色+右旋,父在右,右旋+變色+左旋
四 紅黑樹左旋規則詳細總結

五 紅黑樹插入規則詳細總結

六、心得體會
HashMap的源碼在1.7和1.8兩個版本變化很大,建議大家如果看的話先看1.7的源碼,再看1.8的源碼。說實話,剛開始我1.7的源碼都看不懂,后來找了個講jdk1.7中HashMap源碼視頻,講的很不錯,看完視頻后,再自己看一遍源碼,就很有感覺了。之后看1.8源碼我沒有看過視頻,自己就能看懂了
所以說實話,對于紅黑樹的平衡規則我沒有參考其他任何人寫的文章,我也嘗試看看別人寫的關于紅黑樹的文章,但是我還是覺得這些節點變色旋轉過程太復雜,要通過文章看懂并且記住很有難度,所以我選擇了看源碼自己總結規律
后來把這些過程全部搞懂了,并且也記下了,是通過理解+技巧結合記下的,這個技巧在我這個文章中也要提到,不是死記硬背的
最后一定要像我一樣把自己學到的記錄下來,方便自己看,也分享給需要的人看,這是一舉兩得的事情。
七、寫給讀者的話
接下來,我會總結HashMap紅黑樹刪除時的平衡規則,到時候也會分享出來,希望大家多多關注哦
如何文章中哪里有錯誤,或者有疑問,大家一定要在評論區寫下來,我會及時答復大家和修改錯誤的,謝謝啦
作者:myboy
鏈接:https://juejin.im/post/6876350595305996301
來源:掘金
著作權歸作者所有。商業轉載請聯系作者獲得授權,非商業轉載請注明出處。






