趨膚效應的影響
在長直導體的截面上,恒定的電流是均勻分布的。對于交變電流,導體中出現自感電動勢抵抗電流的通過。這個電動勢的大小正比于導體單位時間所切割的磁通量。以圓形截面的導體為例,愈靠近導體中心處,受到外面磁力線產生的自感電動勢愈大;愈靠近表面處則不受其內部磁力線消長的影響,因而自感電動勢較小。這就導致趨近導體表面處電流密度較大。由于自感電動勢隨著頻率的提高而增加,趨膚效應亦隨著頻率提高而更為顯著。當頻率很高的電流通過導線時,可以認為電流只在導線表面上很薄的一層中流過,這等效于導線的截面減小,電阻增大,大大降低了導體材料的有效利用率。
定義
當交變電流通過導體時,導體內部實際上沒有任何電流,電流集中在臨近導體外表的一薄層 ,這一現象稱為趨膚效應(也稱集膚效應)。

趨膚效應具體解析
在計算導線的電阻和電感時,假設電流是均勻分布于他的截面上。嚴格說來,這一假設僅在導體內的電流變化率(di/dt)為零時才成立。另一種說法是,導線通過直流(dc)時,能保證電流密度是均勻的。但只要電流變化率很小,電流分布仍可認為是均勻的。對于工作于低頻的細導線,這一論述仍然是可確信的。但在高頻電路中,電流變化率非常大,不均勻分布的狀態甚為嚴重。高頻電流在導線中產生的磁場在導線的中心區域產生最大的感應電動勢。由于感應的電動勢在閉合電路中產生感應電流,在導線中心的感應電流最大。因為感應電流總是在減小原來電流的方向,它迫使電流只限于靠近導線外表面處。這樣,趨膚效應使導線型傳輸線在高頻(微波)時效率很低,因為信號沿它傳送時,衰減很大。
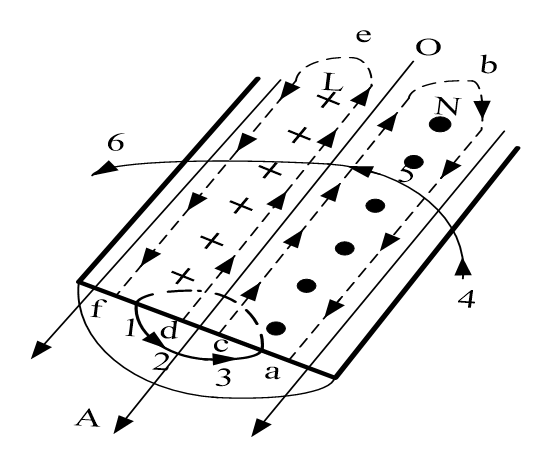
如圖所示,當導體通過高頻電流i時,變化的電流就要在導體內和導體外產生變化的磁場(圖中1-2-3和4-5-6)垂直于電流方向。根據電磁感應定律,高頻磁場在導體內沿長度方向的兩個平面L和N產生感應電動勢。此感應電勢在導體內沿長度方向產生的渦流(a-b-c-a和d-e-f-d)阻止磁通的變化。可以看到渦流的a-b和e-f邊與主電流O-A方向一致,而b-c邊和d-e邊與O-A相反。這樣的主電流和渦流之和在導體表面加強,越向導線中心越弱,電流趨向于導體表面。這就是趨膚效應。
趨膚深度
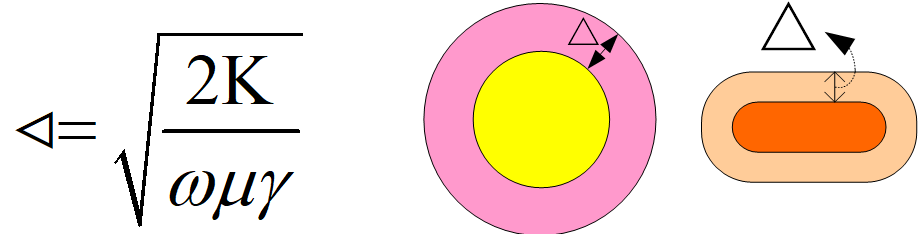
由趨膚效應,我們不難聯想到另一概念—趨膚深度。工程上定義從導體表面到電流密度下降到導體表面電流密度的0.368(即1/e)的厚度為趨膚深度或穿透深度△,即認為導體表面下深度為△的厚度導體流過導線的全部電流,而在△層以外的導體完全不流過電流(在不規則導體中,考慮趨膚深度以最窄邊為準)。△與頻率f(w)和導線物理性能的關系為:

式中,μ-導線材料的磁導率;
γ=1/ρ-材料的電導率;
&KAppa;-材料電導率(或電阻率)溫度系數;對于銅μ=
μ0=4π×10-7H/m; 20℃時ρ=0.01724×10-6 Ω/m,電阻率溫度系數為1/234.5(1/℃),Κ=(1+(T-20)/234.5)。
T-導線溫度(℃)。銅導線溫度20℃、不同頻率下的穿透深度:

一般磁性元件的線圈溫度高于20℃。在導線溫度100℃時,ρ100=2.3×10-6 Ω/cm,穿透深度


降低趨膚效應的方法
由于電流趨膚效應的存在,使得導線的有效載流面積減小,導線對交流電流的電阻大于導線的電阻(這里所說的導線的電阻即為導線對直流電流的電阻);只有導線的趨膚效應面積和導線本身的截面相等時,導線的交流電阻最小,此時有:
Sf =S Rac =Rdc
式中Sf -- 交流趨膚效應面積
S -- 導線截面面積
Rdc -- 導線的直流電阻
Rac -- 導線的交流電阻
因此,減低趨膚效應電阻的最直接的方法,就是改變導線截面的形狀,盡量使趨膚效應面積和導線截面面積相同。
(*在計算圓導線和扁導線的交流趨膚效應電阻時,設定趨膚深度條件為小于圓線半徑或扁線窄邊高度的1/2,在趨膚深度大于這個設定時,計算趨膚效應電阻是無意義的)
1、用多股細線并聯代替單根導線來減低趨膚效應的影響:
對于直徑為D的圓銅導線,如果傳送電流的頻率為 f (Hz),保持交流載流密度Jf 和直流載流密度J 相當,最佳降低趨膚效應電阻的方法是用多股細線替換,使Sf=S,每股細線的直徑為:
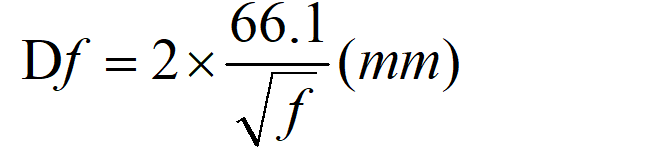
細線的股數為:
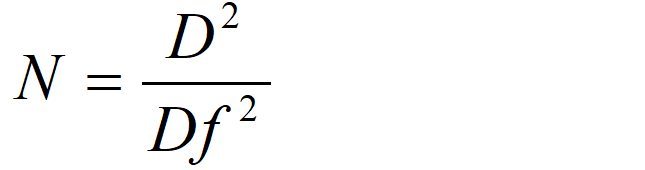
例如,電流 I = 10A,電流密度J = 5.66A/mm2,單股導線的直徑為:

導線的直流電阻最為:Rdc =0.01 x L
(*Rdc =ρ x [ 1 + k x ( T -20 ) ] x L / S;
ρ 銅=0.01749Ωm/mm2;k 是導體材料隨溫度的變化系數,為0.00393) 當電流頻率 f = 100kHz時,趨膚效應深度:

趨膚效應面積:Sf =πx ( D - d ) x d=0.8472 mm2
趨膚效應電阻(20℃時):Rac =0.021 x L (*Rac =ρ x [ 1 + k x ( T -20 ) ] x L / Sf)
交流載流密度:Jf =I/Sf=11.803 A/mm2
用細線代替時,每股線的直徑df 和截面積 Sfn為:df =2 x d =0.42 mm
Sfn =πx df 2 / 4 =0.13726 mm2
股數:N =D2 / df 2 =12.87≈13
用細線代替后,每股電流 In 和電流密度Jn為:In =I/N=0.7769 A
Jn =In/Sfn=5.66 A/mm2
趨膚效應電阻(20℃時):Rac =0.01749 x L / ( N x Sfn )=0.01x L≈Rdc
結論:
用1 根1.50mm直徑的圓銅線,傳送100kHz 10A電流時,電流密度是直流的2.085倍,交流電阻是直流電阻的2.1倍,交流損耗也是直流損耗的2.1倍;使用13根0.42mm直徑的圓導線并聯來代替1.50mm的單根導線時,交流電阻,電流密度,交流損耗和直徑1.50mm的導線的直流電阻,直流電流密度和損耗相當。
2、用帶狀導線來減低趨膚效應的影響:
在大電流時經常使用扁銅線,在可能的情況下,可以將導線的厚度減小,寬度增加,使其變成帶狀,只要合理的確定帶狀線的厚度和寬度,就可以使其高頻趨膚效應的影響最小。
根據扁線最佳高度a = 2 x d 的原則,帶狀銅線的最佳厚度為:

寬度則由要求的電流密度確定。
對于厚度為 a 的帶狀線,如果傳送電流的頻率為 f (Hz),保持交流載流密度Jf 和直流載流密度J 相當,得到最佳減低趨膚效應電阻的帶狀寬度W是:

例如,電流 I = 100A,電流密度J = 5.0A/mm2,單股扁線的截面積是:
S =I/J=100/5=20.0 mm2
導線的直流電阻最為:Rdc =0.8745 x L mΩ
當電流頻率 f = 100kHz時,趨膚效應深度:

如果使用 a=2mm,b= 10mm的扁線時,其有效載流面積為:
Sf =2 x d x ( b + a - 2 x d )=4.842mm2
交流載流密度:Jf=I/Sf =20.65 A/mm2
趨膚效應電阻(20℃時)變為:Rac ≈3.6122 x LmΩ 。
當用帶狀導線代替扁線時,帶的最佳厚度為:a =2 x d =0.42 mm
趨膚效應面積應和扁線面積相同:Sf =a x W =S=20.0mm2
則有帶的寬度為:W =S / a≈48 mm
此時,趨膚效應電阻(20℃時):Rac ≈0.8676 x L mΩ (此時帶狀導線的截面積為a x W=20.16,所以此時Rac比Rdc稍小一點點)
交流載流密度:Jf=I/S =I/ (a x W)=4.96 A/mm2
帶狀線(0.42mm x 48mm)的高頻電流密度和交流電阻僅為原扁線(2mm x 10mm)的1/4;當然,帶狀線的交流損耗也僅為扁線的交流損耗的 1/4 。
結論:
扁狀導線的趨膚效應電阻和導線的截面形狀有關,在截面面積確定后,其窄邊高度越大,趨膚效應的影響也越大。
當根據電流的趨膚深度來確定扁線的窄邊高度,使扁線變成為厚度等于2倍的趨膚深度,而截面面積和原扁線截面面積相等的帶狀后,可以使電流趨膚效應的影響減到最小。

3、利用管和泊減低趨膚效應的影響:
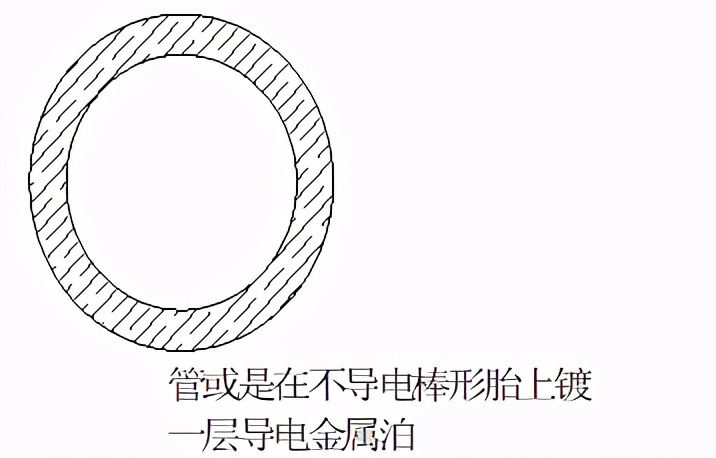
在頻率很高時(至少大于1KHZ),趨膚效應深度也很小,電流基本集中在導體的表面,內部的導體部分基本上沒有電流,將這部分導體去除變成管后,可以大大減輕導體的重量,而對電流的傳送又沒有影響。同樣,在很高的頻率時,也可以將帶狀線壓成泊狀,既保證其對電流的傳送,又可減輕其重量。例如,高頻大功率的傳輸線和高頻天線的振子就可以使用銅管或鋁管來制作,如果在銅管或鋁管的表面加鍍一層高導電的金屬膜(銀或金),效果就會更好;高頻傳輸線或天線,也可以用在不導電的管或棒形胎表面敷(或鍍)導電金屬泊(膜)來制作,即節省昂貴的金屬材料,又保證了導電性能和機械強度。
現在,電子設備的體積越來越小型化,因此電源的工作頻率越來越高,為了提高電源中必需的變壓器和功率電感的效率,一方面使用高頻極低損耗的磁材,一方面使用減低高頻電流損耗的導體;比如,目前已廣泛生產和使用的極扁帶狀漆包線就是一種選擇。