關(guān)注國產(chǎn)芯片事業(yè)的你,一定有很多困惑,能讓大國科技舉步維艱的技術(shù),到底是有多難?
其實(shí),芯片這個東西,說難是真難,就拿5nm光刻機(jī)來說,10多萬個零部件組成,一個一個數(shù)一遍,可能大部分我們現(xiàn)在都不能生產(chǎn)。
可是,芯片說簡單也簡單,從原理上來說,只要你有一定的知識基礎(chǔ),都能搞清楚。在這一點(diǎn)上還確實(shí)是“科技無國界”。至少到現(xiàn)在,相關(guān)的書籍、論文等知識都是能夠公開獲取到的,差的主要就是產(chǎn)業(yè)經(jīng)驗(yàn)和技術(shù)實(shí)力。
今天,我就和大家一起看看芯片到底有多簡單,本文的目標(biāo)是科普一些基本數(shù)學(xué)知識,然后設(shè)計一個最簡單的芯片!
芯片的基礎(chǔ)
芯片,作為最重要的半導(dǎo)體產(chǎn)品,實(shí)現(xiàn)了特定功能。比如電腦CPU實(shí)現(xiàn)了計算、顯示、讀寫內(nèi)存硬盤數(shù)據(jù)、接受鼠標(biāo)鍵盤輸入等等豐富的功能。
那大家有沒有想過,芯片的基礎(chǔ)是什么?
可能有人馬上會想到硅,硅作為半導(dǎo)體材料是芯片的基礎(chǔ)。可是喝水的玻璃杯也有硅呀,它就不值錢,所以硅不是根本基礎(chǔ)。芯片為什么要用硅?是因?yàn)橐诠枭厦嬷圃旒呻娐罚」璧奶攸c(diǎn)是能在很小的面積上集成大量的電路器件。
這么說芯片的基礎(chǔ)是電路?電路有很多種,家里的燈泡和開關(guān)也組成一個電路,這和芯片沒啥關(guān)系。芯片用到的是邏輯電路。
再試一次,芯片的基礎(chǔ)是邏輯電路?呃,已經(jīng)很接近了,但是還不是,邏輯電路是做邏輯運(yùn)算的,邏輯運(yùn)算也叫布爾代數(shù)運(yùn)算。
所以,芯片的根本基礎(chǔ)是數(shù)學(xué)!更具體的說是布爾代數(shù)!
這個結(jié)論一點(diǎn)兒也不奇怪,大家都知道物理學(xué)的基礎(chǔ)是數(shù)學(xué),就連偉大的物理學(xué)家牛頓都和阿基米德、高斯一起并稱世界三大數(shù)學(xué)家。
布爾代數(shù)
了解最基本的布爾代數(shù),你就會知道機(jī)器是怎么運(yùn)算,也就明白了芯片要怎樣設(shè)計。
接下來我就介紹一下二進(jìn)制和布爾代數(shù),下面的內(nèi)容爭取讓小朋友都能明白。
為什么能讓小朋友都明白呢?因?yàn)閿?shù)學(xué)家布爾本人,就沒上過大學(xué),靠自學(xué)成才,并在19歲開辦了一所小學(xué),經(jīng)營了10多年。他認(rèn)為自己最主要的職業(yè)是教師,他的愿望是幫孩子們找到理解和掌握復(fù)雜規(guī)律的方法。
布爾代數(shù)的起源,是希望用數(shù)學(xué)表達(dá)人的邏輯思維。
其中和計算機(jī)相關(guān)的是幾個重要的布爾運(yùn)算:
1、與 運(yùn)算
舉個例子:我喜歡吃烤羊肉串
我們讓A代表燒烤,B代表羊肉串。
則上面的表達(dá)變?yōu)榱耍?/p>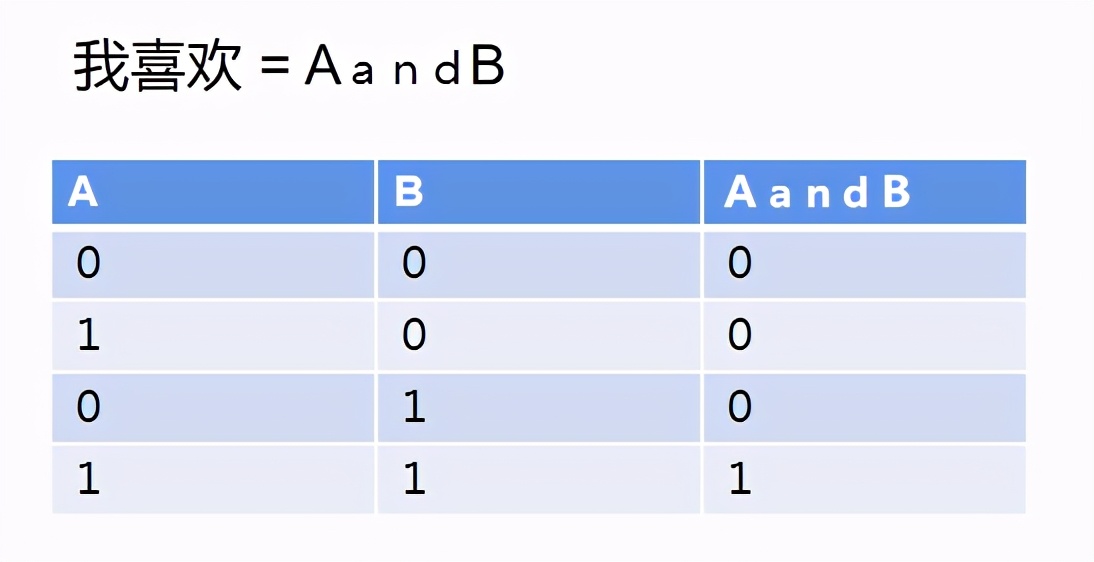
A和B都是真,做運(yùn)算的結(jié)果才是真。比如,烤牛肉串,就是A=1,B=0,AandB=0。所以我不喜歡烤牛肉串。
2、或 運(yùn)算
舉個例子:我喜歡吃燒烤或是火鍋。
我們讓A代表燒烤,B代表火鍋。
則上面的表達(dá)變成了:
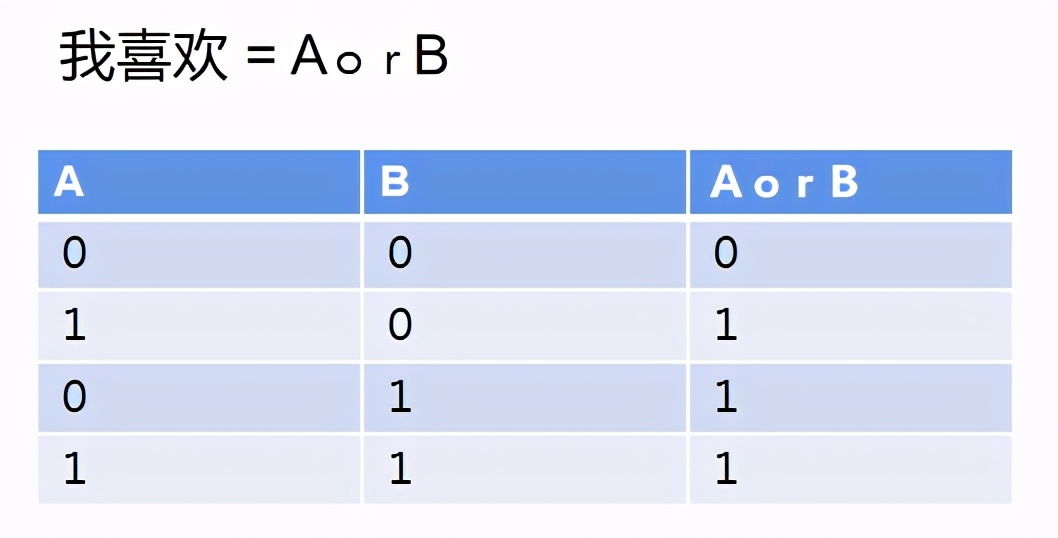
不管是燒烤還是火鍋,只要有一個我就吃,當(dāng)然兩樣都來更好!
3、非 運(yùn)算
舉個例子:我不喜歡吃辣。
我們讓A代表辣。
則上面的表達(dá)變成了:
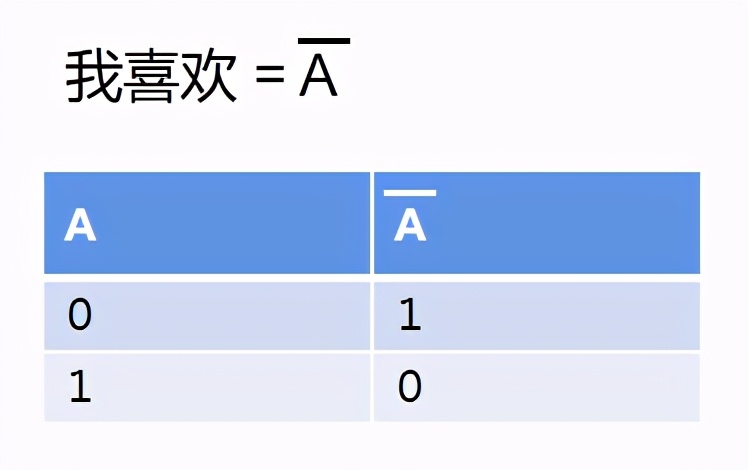
4、異或 運(yùn)算
舉個例子:我最喜歡吃燒烤和冰激凌,但是一起吃會拉肚子。
我們讓A代表燒烤,B代表冰激凌。
則上面的表達(dá)變成了:
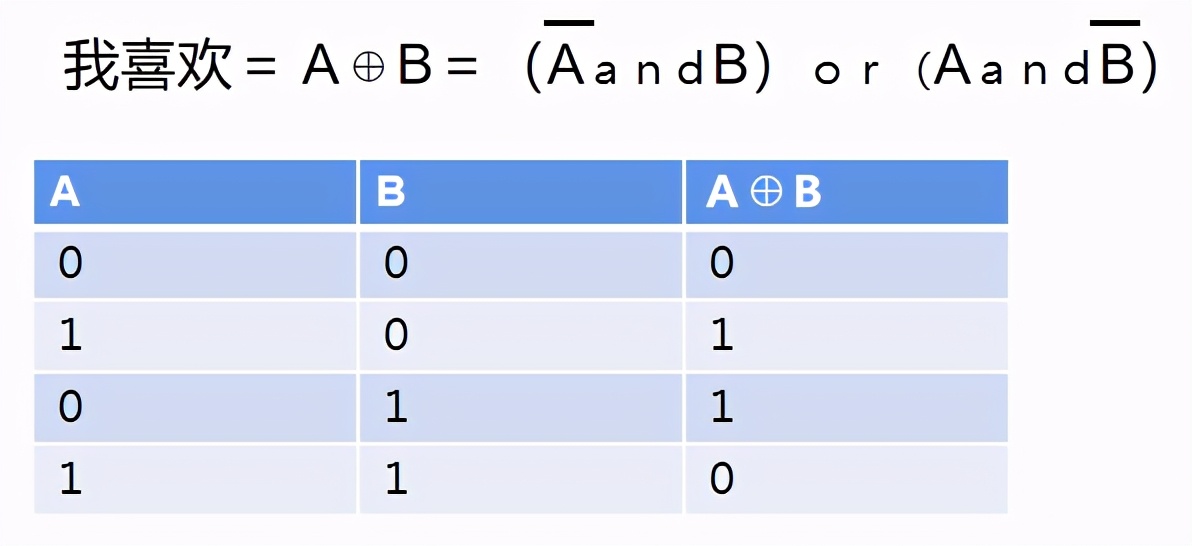
理解這個運(yùn)算可能有點(diǎn)兒難,啥意思呢?就是A和B不能一樣,沒有燒烤沒有冰激凌肯定不行,可是一起來也承受不了!
除了上面4種布爾運(yùn)算,還有與非、或非、異或非運(yùn)算。從異或運(yùn)算可以看出,全部的運(yùn)算都可以由與、或、非運(yùn)算結(jié)合產(chǎn)生。
二進(jìn)制運(yùn)算
咱們接著講二進(jìn)制運(yùn)算。
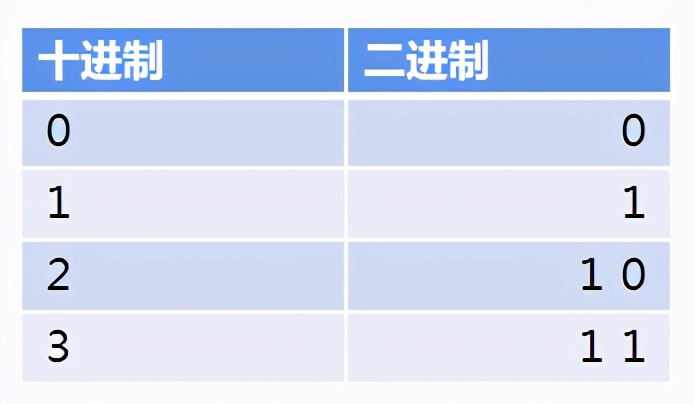
二進(jìn)制就是用0、1表示一切數(shù)字,每一位上只能是0和1,到了2就要進(jìn)位。
比如,十進(jìn)制的2,用二進(jìn)制表示就得進(jìn)位了,變成兩位數(shù)10,而十進(jìn)制3就是11。
二進(jìn)制是德國數(shù)學(xué)家萊布尼茨在300多年前發(fā)明的,那個時候連計算機(jī)的影子還沒有,到底萊布尼茨為啥要發(fā)明一個當(dāng)時根本沒用的二進(jìn)制,說實(shí)話沒人能搞清楚。
說起二進(jìn)制,不得不說一下我國的八卦,不是到處亂講的那種娛樂圈八卦,而是真正的八卦。
八卦講究的是兩儀生四象,四象生八卦:

看到?jīng)]有,很多人認(rèn)為八卦就是二進(jìn)制的先驅(qū)。兩儀是陰陽,也就是0和1,四象是二進(jìn)制兩位數(shù),八卦是二進(jìn)制三位數(shù),而伏羲64卦就是二進(jìn)制的六位數(shù):
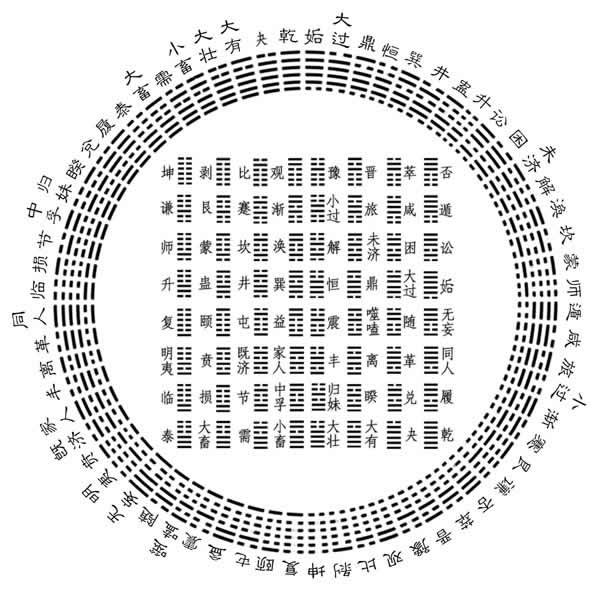
貌似道理還真是一樣,咱們的老祖先當(dāng)時基于什么發(fā)明的八卦,說實(shí)話這也搞不清楚。
可有人卻翻出了當(dāng)時萊布尼茨和一位在北京生活的傳教士的信,來試圖證明萊布尼茨發(fā)明二進(jìn)制是受了中國八卦的啟發(fā),而且很多人都信了這個說法。
實(shí)際的過程是這樣的:當(dāng)時萊布尼茨給這位傳教士寫信,希望他向康熙皇帝介紹二進(jìn)制,這個傳教士一看,這不就是中國的八卦么,給萊布尼茨回信說了八卦的情況。然后萊布尼茨寫了一篇文章論述二進(jìn)制在中國的實(shí)際應(yīng)用。
萊布尼茨到底受沒受八卦啟發(fā),都是猜測,就算萊布尼茨受了八卦的啟發(fā),那又怎樣?在萊布尼茨發(fā)明二進(jìn)制的時候,我們的康熙大帝正在打吳三桂呢,我們的現(xiàn)代文明還沒有開化。
所以,關(guān)于八卦和二進(jìn)制的事,我們就當(dāng)它是八卦好了,咱們接著說二進(jìn)制計算。
假設(shè)有兩個一位的二進(jìn)制數(shù)要相加,那么會有四種可能:
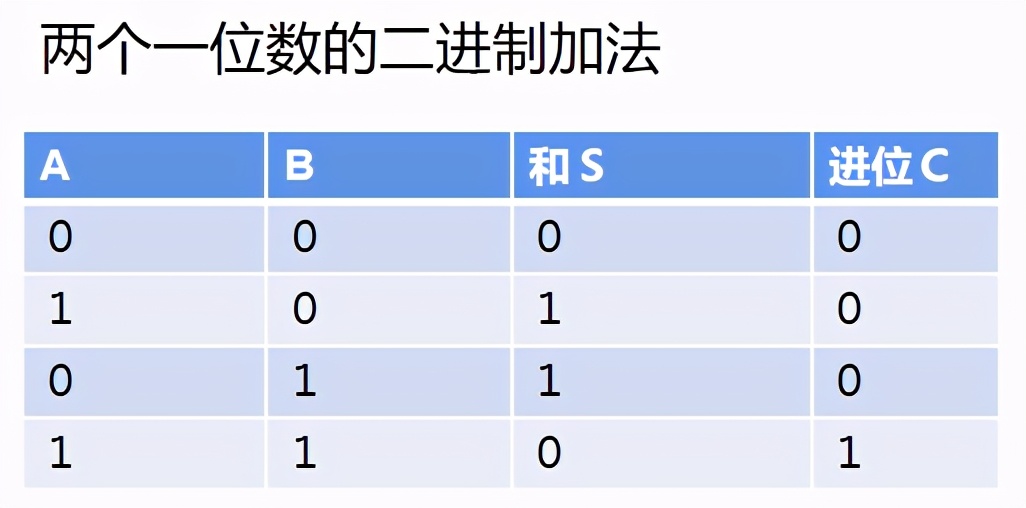
前三種情況不需要進(jìn)位,后一種情況和S是一個兩位二進(jìn)制數(shù),所以需要進(jìn)位,我們單獨(dú)設(shè)置一個進(jìn)位標(biāo)識C。
大家發(fā)現(xiàn)沒有,二進(jìn)制的加法和上面介紹的布爾運(yùn)算是一樣的:
- 加法的和就是兩個加數(shù)的異或運(yùn)算
- 加法的進(jìn)位標(biāo)識就是兩個加數(shù)的與運(yùn)算
我們用布爾運(yùn)算符做個邏輯圖,就是這樣的:
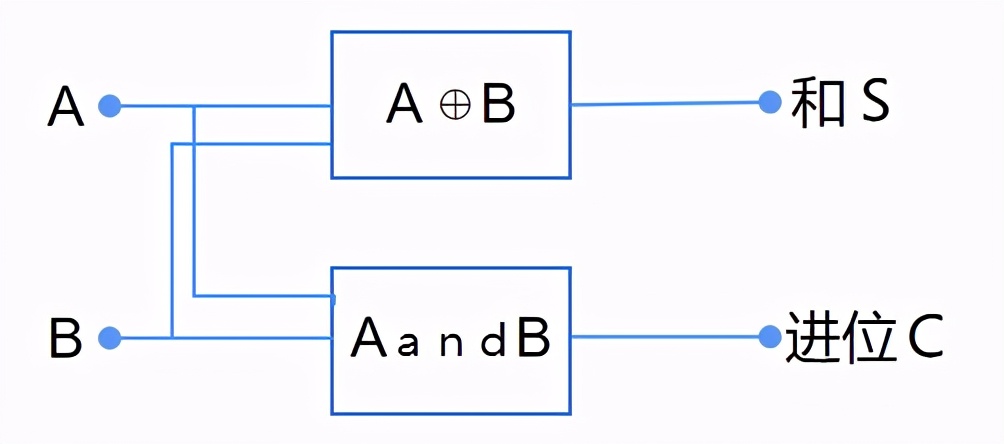
上面就是一個用布爾運(yùn)算符表示的半加器,可以進(jìn)一步表示如下:
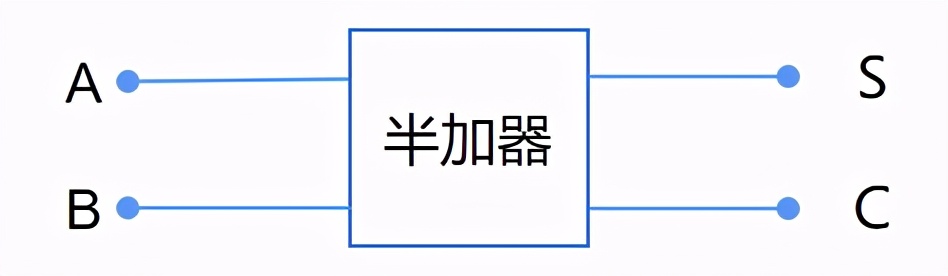
為什么叫半加器呢?這是因?yàn)橛嬎鉇+B的時候,沒有考慮上一位有沒有進(jìn)位的情況,所以這個半加器只能計算二進(jìn)制數(shù)最末一位上的加法。
如果A和B不是末位上的數(shù),那就要考慮前一位的計算結(jié)果有沒有進(jìn)位(Cin是上一位的進(jìn)位標(biāo)識,Cout是當(dāng)前位計算完向上一位的進(jìn)位情況),會有8種情況:
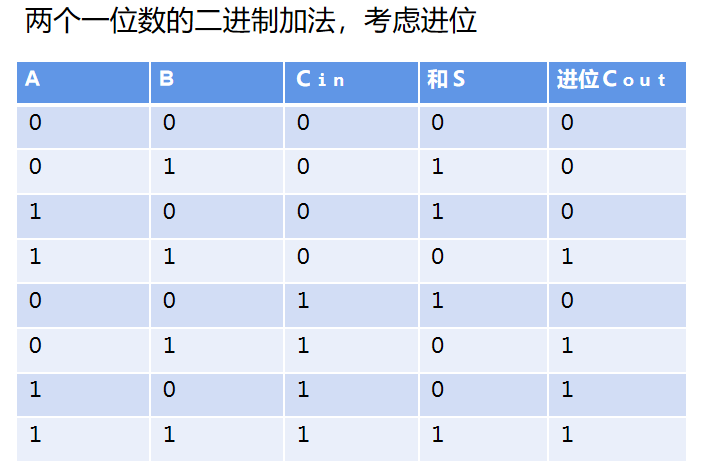
這個過程可以通過2個半加器和一個或運(yùn)算來實(shí)現(xiàn):
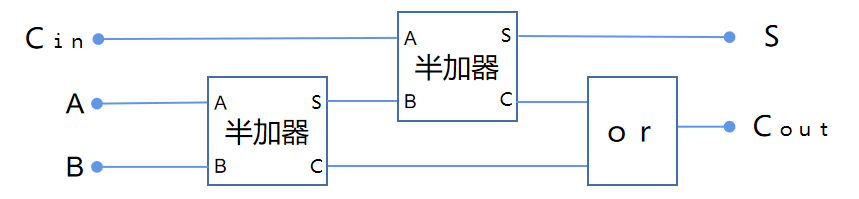
這就是全加器:
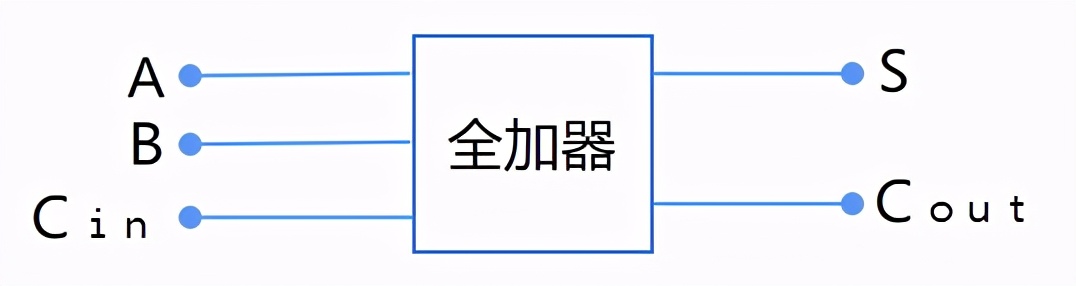
看,我們只用布爾代數(shù)的四個運(yùn)算符,就實(shí)現(xiàn)了一位二進(jìn)制數(shù)的加法。
其實(shí),我們只用了三個運(yùn)算符,因?yàn)楫惢蜻\(yùn)算可以畫成與、或、非運(yùn)算的組合,當(dāng)然這樣太麻煩。
全加器也是一樣,如果我們不怕麻煩,可以細(xì)致的畫成異或、與、或運(yùn)算的組合。
八位二進(jìn)制加法器
大家看吧,關(guān)于計算機(jī)的數(shù)學(xué)也不難。
接下來最神奇的要來了,我們要用剛剛學(xué)到的布爾代數(shù)知識,設(shè)計一個最簡單的芯片。
這是一個能夠進(jìn)行八位二進(jìn)制數(shù)加法的加法器。
這還是有一些挑戰(zhàn)的,這個加法器,如果做出來也算是一個最簡單的芯片,真的是芯片哦!
這個加法器的輸入是2個八位二進(jìn)制數(shù):
一個用A表示,八位分別是A[0],......,A[7];
另一個用B表示,八位分別是B[0],......,B[7];
還有一個輸入是進(jìn)位標(biāo)識Cin,如果這個加法器單獨(dú)使用時,這個輸入始終置0。
輸出是S,八位分別是S[0],......,S[7];
輸出進(jìn)位標(biāo)識是Cout。
下面請大家看看,這個加法器到底是什么樣子:
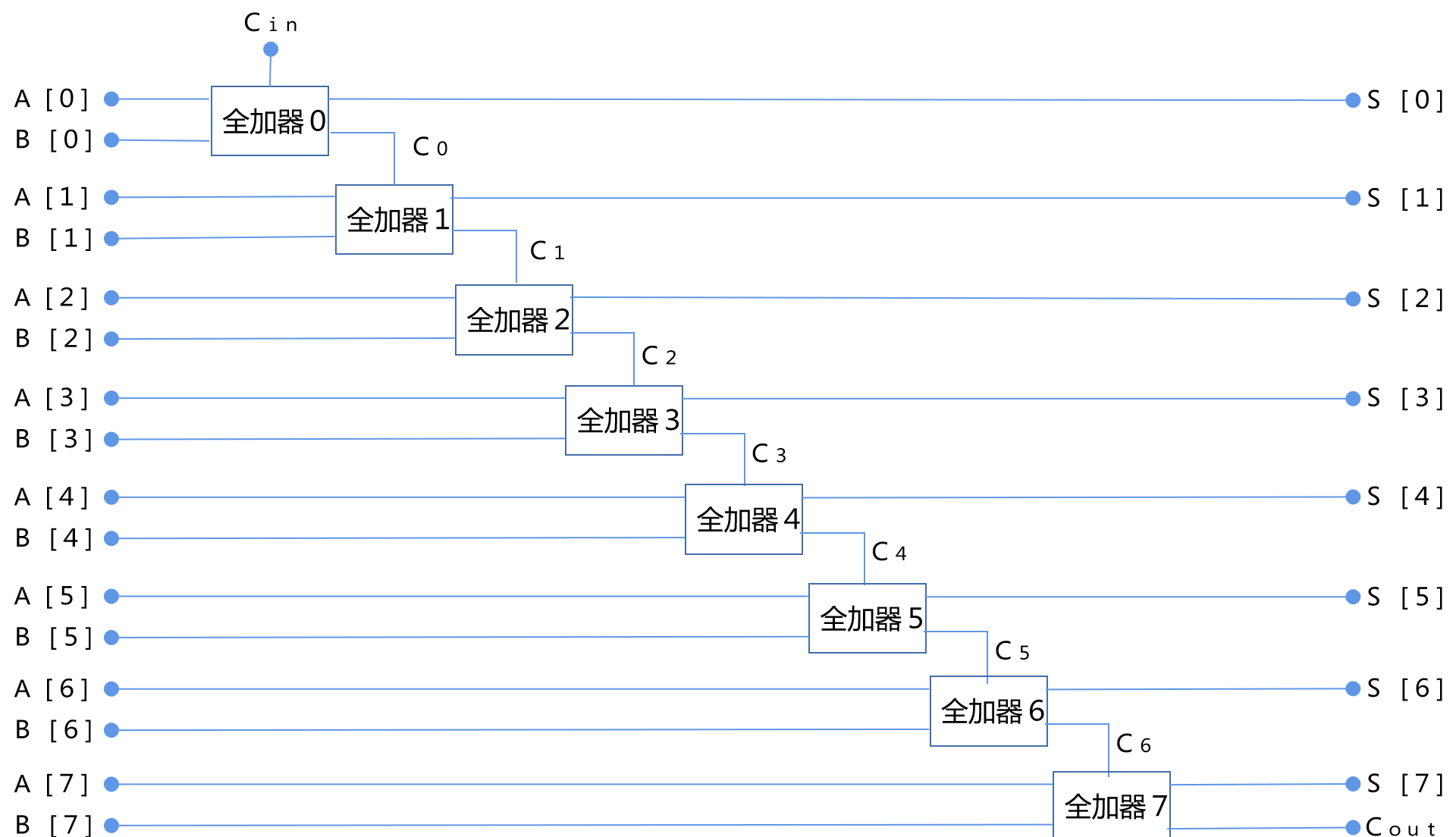
這就是一個用8個全加器構(gòu)成的八位二進(jìn)制加法器,神奇不神奇?
我們沒有添加任何其他的東西,就是剛剛學(xué)過的全加器,如果大家有興趣,可以把每個全加器用2個半加器和一個或運(yùn)算符展開。
進(jìn)一步可以再把每個半加器用異或運(yùn)算符和與運(yùn)算符展開,不知道哪位讀者有興趣,反正用手畫,我是會崩潰的。
而這一切,在芯片設(shè)計的時候,都是由EDA軟件來完成。
后續(xù)工作
到此,我們已經(jīng)在邏輯上設(shè)計了一個功能最簡單的八位二進(jìn)制加法芯片。
為什么要說是邏輯上呢?因?yàn)榈侥壳盀橹梗覀冞€沒有用到任何電路知識。所涉及的全部是布爾代數(shù)知識,所以這個芯片是邏輯上可行,但是還無法制造。
那怎么做出實(shí)際能用的芯片呢?
首先我們需要有和上面布爾運(yùn)算符對應(yīng)的電子元件,實(shí)現(xiàn)同樣的功能。然后按照設(shè)計把這些元件連接起來。這樣就有了實(shí)際的電路,這種電路就叫門電路。實(shí)現(xiàn)了上面布爾運(yùn)算的元件就叫門元件。
最終,我們要在硅片上面制作出這種門元件,這樣就在硅片上面實(shí)現(xiàn)了門電路,也就是集成電路。
最后,再把這個集成電路切割下來,把輸入輸出引腳做好,然后封裝,一個完整的芯片就產(chǎn)生了!
所有這些后續(xù)的工作,我都會在接下來的文章一點(diǎn)兒一點(diǎn)兒和大家一起學(xué)習(xí)!
如果您對我的文章感興趣,歡迎關(guān)注我!
謝謝!






